詳細一點的 Neural Network

昨天有提到 Logistic Regression 的數學形式：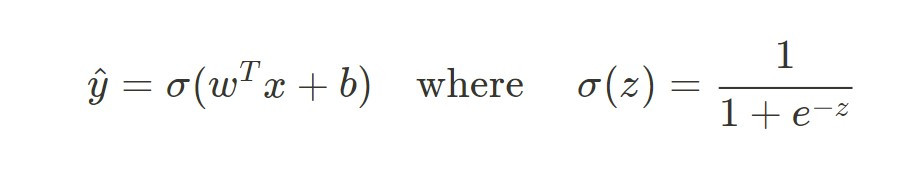

配合 NN 的圖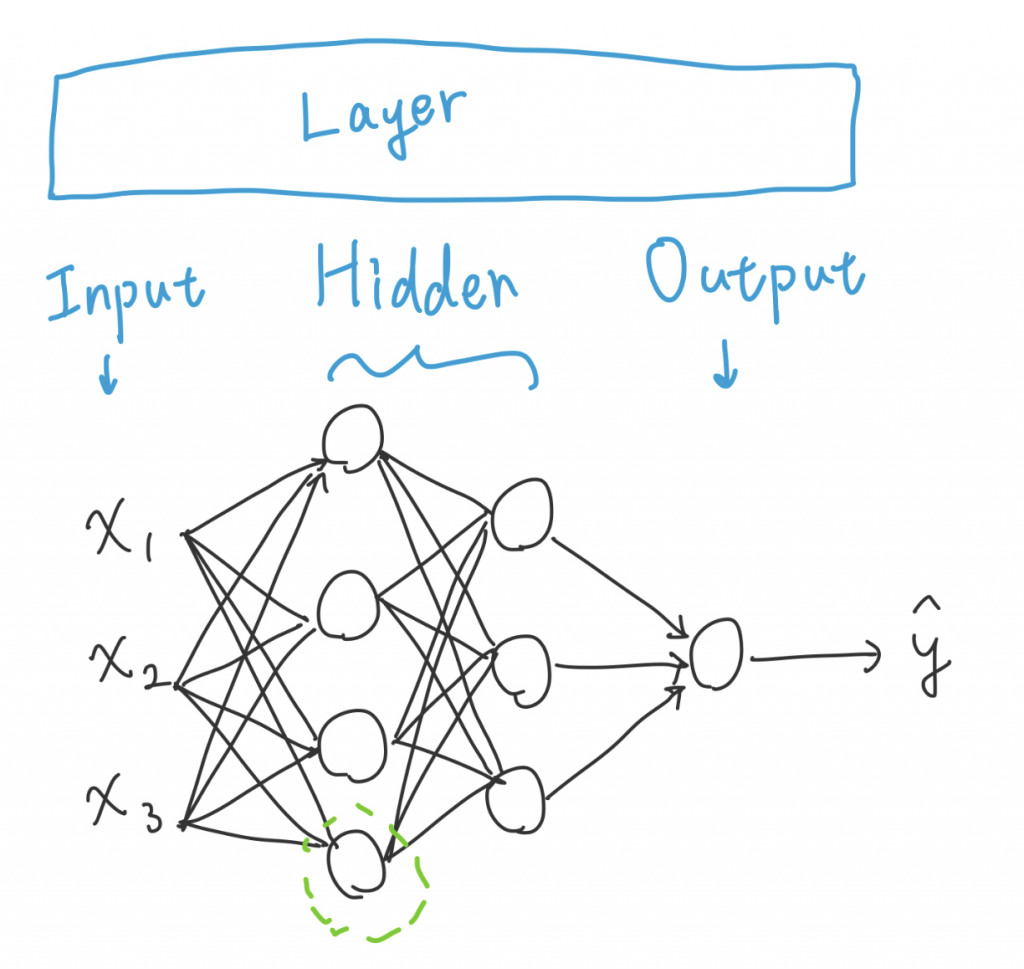

這裡可以看到三個 Layer

1. Input layer：輸入的 Data(圖片)，這一層不會納入 NN 的層數
2. Hidden layer：夾在 Input 和 Output 之間的 Neuron 皆屬於這一層
3. Output layer：最後輸出

其中 Input layer 不會納入 NN 的層數計算(或是說稱作第零層)，因此上圖為 3 層的 Neural Network

Neuron 裡的運算

加上數學式實際上的會長怎麼樣呢？因為現在是 NN，我們把上面那個在摯友的 Neuron 放大來看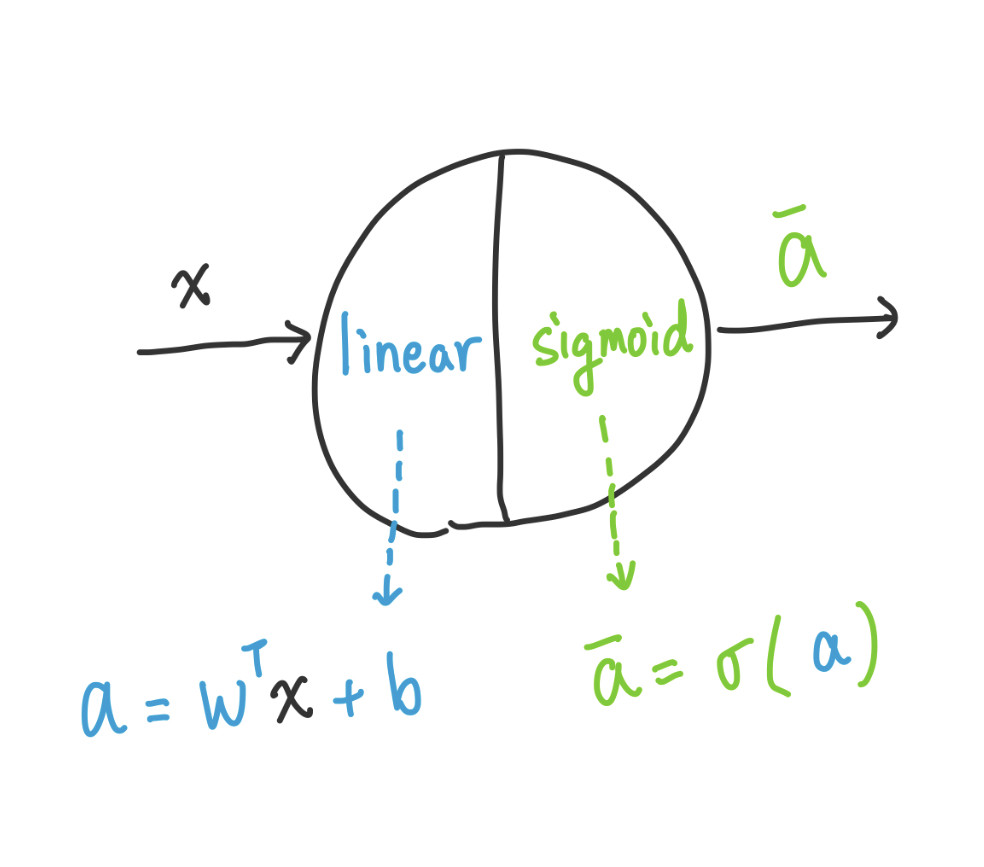

左半邊為線性函數，其中 w, b 皆為參數，我們需要找到這兩個最適合的值
右半邊則為非線性函數 Activation function，而我這邊選擇 Sigmoid function 作為 Activation function

Note

• 若是少了 Activation function 會發生甚麼事？

會爆炸。正確來說是只剩下左半邊的線性函數，每個 Neuron 都這樣做，左邊的 Output 是右邊的 Input，從頭做線性到尾，出來的結果也會是線性，那代表：這個模型就不能做非線性的預測了！
這個模型的使用度直接大幅下降，因此 Activation function 很重要的

Activatoin function

這邊不是只能選擇 Sigmoid 作為激活函數，也可以嘗試使用 tanh

希望大家都還記得，忘記就算了反正很少用，但到了大四突然冒出三角函數微分跟積分的時候，早就忘記那種東西了，結果還突然冒出 tanh 出來搗亂，就會很頭痛

不過 Sigmoid 和 tanh 以圖形來說都有一個小缺點：在距離 0 較遠的地方都會收斂得很慢，Gradient Descent 會跑超慢
圖形：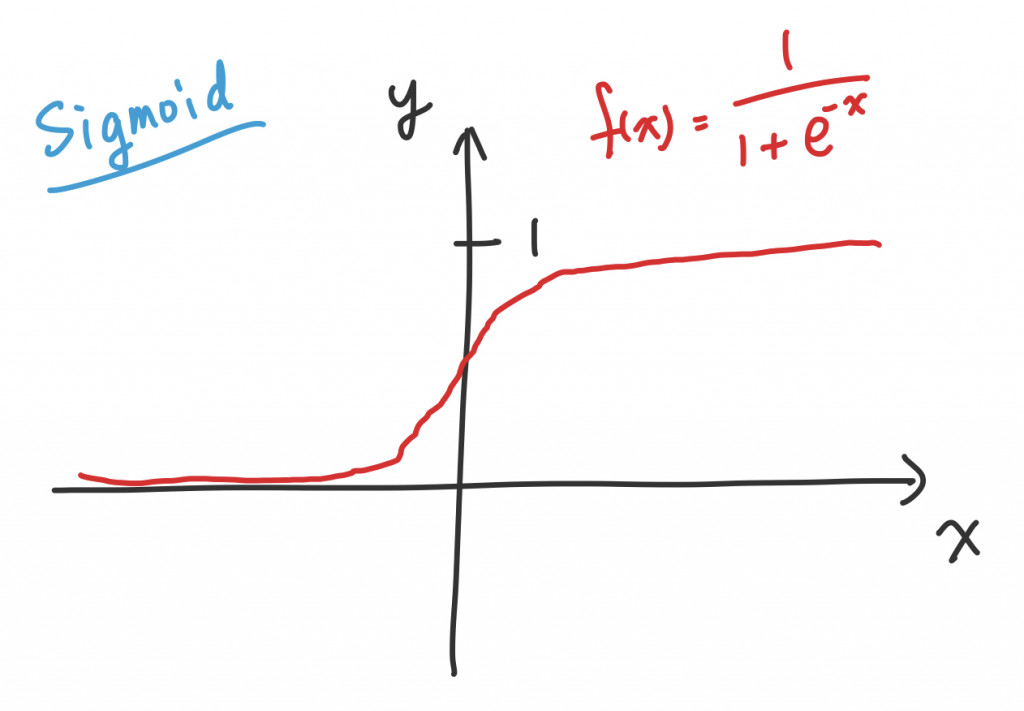

因此我們要來介紹 ReLU 這個神奇小東西

ReLU

Rectified Linear Unit 的數學式子為：
圖型：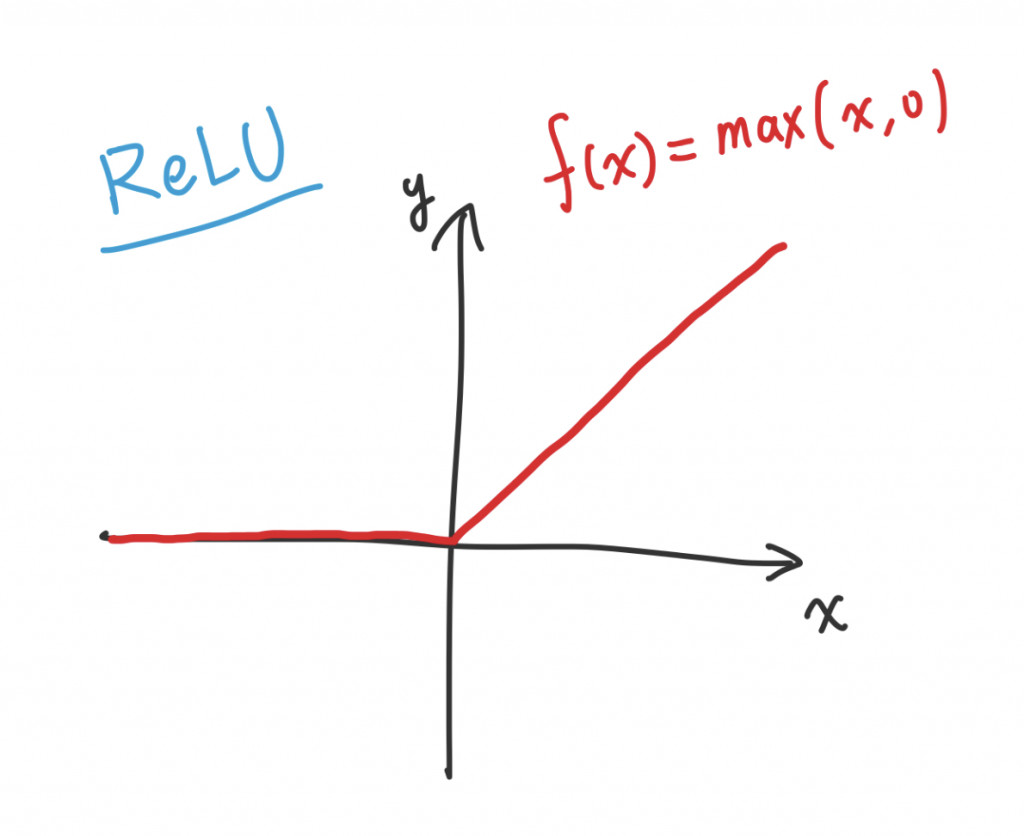

有了 ReLU 就可以解決 Gradient Descent 的問題，效能也不錯，是個好東西！

小心得

後半部寫得比較快了，但還是花了一個半小時，與其去找別人的圖，倒不如自己畫，還不用附上參考連結
還沒講 Gradient Descent 不知道會不會有不清楚的地方，其實原本的課程是先講 GD 再說 NN
明天繼續努力，想趕快把筆記的部分處理掉，然後寫 Huggingface 實作遇到的各種奇葩的問題